Snippets
| Autor: | Wojciech Muła |
|---|---|
| Dodany: | 3.03.2002 |
| Aktualizacja: | 7.09.2016 (Petr Kobalicek zauważył błąd w implementacji paddb), 19.08.2008 |
Contents
- Normalizacja wskaźnika
- Powielanie bajtu
- Wzorzec bitowy na maskę
- Transpozycja bitów
- Odpowiedniki rozkazów BT, BTC, BTS i BTR
- Odpowiednik rozkazu BSWAP
- Odpowiedniki rozkazów BSF i BSR
- Konwersja float na int
- Obrót punktu 2D (FPU)
- cxchg — Conditional XCHG (x86)
- nswap — Nibble Swap (x86, MMX)
- Generacja maski
- Mnożenie równoległe (x86)
- Wersja x86 rozkazu paddb
- stricmp
- Population Count
- Implementacja funkcji modf() (FPU)
- Implementacja funkcji pow(x, y) (FPU)
- min/max (cmov)
- Implementacja funkcji intpow(double, int)
- Wyświetlanie liczb floating-point (FPU)
- Extract Bit String
- Mnożenie wektora 4x1 przez macierz 4x4 (FPU)
- x86: równoległe tworzenie maski dla niezerowych bajtów (5.07.2007)
- Tworzenie maski z ustawionymi/wyzerowanymi bitami na młodszych pozycjach (19.08.2007)
Normalizacja wskaźnika
W programach działających w trybie rzeczywistym wynik porównywania wskaźników nie jest jednoznaczny. Jeden adres fizyczny może być reprezentowany przez 4096 różnych adresów logicznych. Liczba adresów logicznych wynosi 232 (segment i offset mają po 16 bitów), natomiast jest zaadresowanie tylko 220 bajtów, co daje 212 powtarzających się adresów.
Adres fizyczny jest 20-bitowy i wyznacza się go ze wzoru:
adres fizyczny = segment*16 + offset = segment << 4 + offset
Normalizacja polega na przypisaniu wartości segmentu 16 najstarszych bitów adresu fizycznego, natomiast przesunięciu 4 najmłodszych, dzięki temu zapis będzie zawsze jednoznaczny.
8086:
; wejście/wyjście: ax - segment = |ssss ssss|ssss ssss| ; dx - offset = |oooo oooo|oooo oooo| mov cx, dx ; cx = |0000 oooo|oooo oooo| shr cx, 4 ; add ax, cx ; ax = znormalizowany segment and dx, 0fh ; dx = znormalizowany offset
80386:
; wejście/wyjście: eax - segment
; edx - offset
and eax, 0000ffffh ; może nie być potrzebne gdy jesteśmy pewni,
and edx, 0000ffffh ; że starsze słowa są równe zero
shl eax, 4 ; adres fizyczny
add eax, edx ;
mov edx, eax
shr eax, 4 ; ax - znormalizowany segment
and edx, byte 0fh ; dx - znormalizowany offset
; tak zapisany rozkaz ma 3 bajty, zamiast 5
; (stała jest rozszerzana ze znakiem)
Powielanie bajtu
Problem przedstawia się następująco: jak mając słowo |00|00|00|aa|, uzyskać |aa|aa|aa|aa|?
x86
Pierwszy sposób, najciekawszy chyba, pokazał Ervin Toth (Ervin/AbaddoN) w magazynie Imphobia #9.
; eax = 0x000000aa
imul eax, 0x01010101 ; zmieniając mnożnik można uzyskać dowolne
; ułożenie bajtu w podwójnym słowie, np.
; 0x00010101 da 0x00aaaaaa
Jeśli mnożenie jest względnie szybkie (3-4 cykle opóźnienia), to jak najbardziej użycie tej metody ma sens, w przeciwnym razie można obyć się bez mnożenia:
; eax = 0x000000ab mov ah, al ; eax = 0x0000abab mov bx, ax shl eax, 16 ; eax = 0xabab0000 mov ax, bx ; eax = 0xabababab
MMX
; eax = |0000|00ab| movd mm0, eax ; mm0 = |0000|0000|0000|00ab| punpcklbw mm0, mm0 ; mm0 = |0000|0000|0000|abab| punpcklbw mm0, mm0 ; mm0 = |0000|0000|abab|abab| ; tutaj już można przesłać zawartość mm0 do rejestru 32-bitowego punpcklbw mm0, mm0 ; mm0 = |abab|abab|abab|abab|
SSE
W SSE dostępny jest rozkaz pshuwf, który rozmieszcza słowa w rejestrze źródłowym zgodnie z indeksami zapisanymi w stałej natychmiastowej:
; eax = |0000|00ab| mov ah, al ; eax = |0000|abab| movd mm0, eax ; mm0 = |0000|0000|0000|abab| pshufw mm0, mm0, 0x00 ; mm0 = |abab|abab|abab|abab|
SSE3
W SSE3 dostępny jest rozkaz pshufb, który rozmieszcza bajty w rejestrze docelowym XMM zgodnie z indeksami zapisanymi w argumencie źródłowym:
; eax = |0000|00ab|
pxor %xmm0, %xmm0 ; wszystkie indeksy równe zero
movd %eax, %xmm1
pshufb %xmm0, %xmm1 ; xmm1 -> na wszystkich pozycjach
; zawartość zerowego elementu xmm1, tj. %al
Wzorzec bitowy na maskę
Problem polega na zamianie wzorca bitowego, np. |0101 1110|, na maskę bajtów, czyli: |00|ff|00|ff|ff|ff|ff|00|. Jednym z zastosowań może być zamiana obrazów 1bpp na 8bpp lub 32bpp.
80386:
;wejście: al = |10100110| ;wyjście: ecx:edx add al, al ; al = |01001100|, CF = 1 = MSB(al) sbb ch, ch ; ecx= |xx|xx|ff|xx| add al, al ; al = |10011000|, CF = 0 -- add al, al jest równoważne shl al, 1 sbb cl, cl ; ecx= |xx|xx|ff|00| shl ecx, 16 ; ecx= |ff|00|xx|xx| add al, al ; al = |00110000|, CF = 1 sbb ch, ch ; ecx= |ff|00|ff|xx| add al, al ; al = |01100000|, CF = 0 sbb cl, cl ; ecx= |ff|00|ff|00| ; -- analogicznie należy postąpić dla edx
MMX:
; wejście: eax = |xx|xx|xx|ab|
; 0xab = 0b10101011
; wyjście: mm0
; niszczy: mm1
segment .data
; maska dla bitów - pozycja bitu jest równa pozycji bajtu
mmx_bits db 1 << 0 ; 0x01
1 << 1 ; 0x02
1 << 2 ; 0x04
1 << 3 ; 0x08
1 << 4 ; 0x10
1 << 5 ; 0x20
1 << 6 ; 0x40
1 << 7 ; 0x80
segment .text
movq mm1, [mmx_bits]
movd mm0, eax ; mm0 = |00|00|00|00|xx|xx|xx|ab|
punpcklbw mm0, mm0 ;
punpcklbw mm0, mm0 ;
punpcklbw mm0, mm0 ; mm0 = |ab|ab|ab|ab|ab|ab|ab|ab|
pand mm0, mm1 ; mm0 = |80|00|20|00|08|00|02|01|
pcmpeqb mm0, mm1 ; mm0 = |ff|00|ff|00|ff|00|ff|ff|
; mm0 = (mm0==mmx_bits) ? 0xff : 0x00
Transpozycja bitów
Celem jest zamiana kolejności bitów w słowie, np. 11001010b -> 01010011b. Może być przydatne przy operacji flipX dla obrazów 1bpp.
Transpozycja bitów w bajcie (1):
; 28-08-01 14:09:29
; wejście: al
; wyjście: bl
; niszczy: cx
mov cx, 8 ; 8 bitów
_transp:
; al = 1000 0011
rol al, 1 ; al = 0000 0111, CF=1
; bl = 0000 0000
rcr bl, 1 ; bl = 1000 0000
loop _transp
Transpozycja bitów w bajcie (2):
; 28-08-01 14:09:29
; wejście: al
; wyjście: bl
; niszczy: cx
mov cx, 8
xor bl, bl
_transp:
shr al, 1 ; CF = LSB(al)
adc bl, bl ; czyli:
; shr bl,bl
; bl[0] = CF
loop _transp
Transpozycja bitów w słowie 32-bitowym:
; wejście: eax
; wyjście: eax
; modyfikuje: ebx
; ebx = ...edcba
mov ebx, eax ; ebx = ...edcba
shr ebx, 1 ; ebx = ....edcb
and eax, 01010101h ; eax = ...e0c0a
and ebx, 01010101h ; ebx = ....0d0b
;
lea eax, [ebx + eax*2] ; eax = ....cdab
; zamień kolejność 2 sąsiednich bitów
mov ebx, eax ; zamień kolejność
shr ebx, 2 ; dwóch sąsiednich pól 2-bitowych
and eax, 03030303h ;
and ebx, 03030303h ;
;
lea eax, [ebx + eax*4] ;
mov ebx, eax ; zamień kolejność
shr ebx, 4 ; tetrad
and eax, 0f0f0f0fh ;
and ebx, 0f0f0f0fh ;
;
shl eax, 4 ;
or eax, ebx ;
bswap eax ; i bajtów
Kod wykorzystujący rozkazy MMX2, przedstawione raczej jako ciekawostka. :-)
; wejście: al
; wyjście: al
; niszczone: eax, mm0, mm1
pxor mm1, mm1
movd mm0, eax ; mm0 = |00|00|00|00|00|00|00|al|
punpcklbw mm0, mm0 ; mm0 = |00|00|00|00|00|00|al|al|
pshufw mm0, mm0, 00h ; mm0 = |al|al|al|al|al|al|al|al|
; w k-tym bajcie zostawiany jest k-ty bit
pand mm0, {80h,40h,20h,10h,08h,04h,02h,01h}
; następnie generowana jest **negacja** maski
pcmpeqb mm0, mm1
; po czym zostawiane są bity na pozycjach 8-k
pandn mm0, {01h,02h,04h,08h,10h,20h,40h,80h}
; na końcu wszystkie bity są łączone w 1 bajt
psadbw mm0, mm0
movd eax, mm0
Z użyciem rozkazów dostępnych w SSSE3 możliwa jest szybka transpozycja bitowa słów 128-bitowych! Zobacz w osobnym artykule.
Odpowiedniki rozkazów BT, BTC, BTS i BTR
W pierwszych procesorach Pentium produkowanych przez Intela te rozkazy były bardzo wolne. Poniżej przedstawiam ich zamienniki.
BT:
; składnia : bt ax, bit
; oryginalna instrukcja: 4 cykle
; poniższy kod : 3 cykle -- pplain
;
; niszczy: bx
mov bx, ax ;
and bx, ~(1 << bit) ; bx = ax and not (1 shl bit)
; Jeśli bit w ax był ustawiony to wartość bx zmieni się (zmaleje!),
; w przeciwnym razie pozostanie niezmieniona.
cmp bx, ax ; CF = bx < ax
BTC, BTR i BTS:
; składnia : btc ax, bit ; btr ax, bit ; bts ax, bit ; oryginalna instrukcja: 7 cykle ; poniższy kod : 3 cykle -- pplain, uwzględniając parowanie instrukcji ; niszczy: bx, cx mov cx, ax ; cx = ax mov bx, ax ; and bx, ~(1 << bit) ; bx = ax and not (1 shl bit) xor ax, 1 << bit ; dla BTC zaneguj, ;and ax, ~(1 << bit) ; dla BTR wyzeruj, ;or ax, 1 << bit ; dla BTS ustaw bit w ax cmp bx, cx ; zobacz komentarz do BT
Odpowiednik rozkazu BSWAP
Któż ma teraz 286? Ale dla sportu można sobie napisać odpowiednik tego rozkazu.:-)
Służy on do zamiany kolejności bajtów w podwójnym słowie, jego głównym zastosowaniem jest konwersja danych pomiędzy konwencjami zapisu little-endian (np. procesory Intela) i big-endian (np. procesory Motoroli, protokoły sieciowe). W zapisie little-endian młodszy bajt znajduje się pod mniejszym adresem.
; wejście: eax
; wyjście: eax
; eax = 0x44332211
xchg al, ah ; eax = 0x44331122
rol eax, 16 ; eax = 0x11224433
xchg al, ah ; eax = 0x11223344
Zamiast rozkazu xchg al, ah można użyć rol ax, 8 (kod autorstwa barta/xtreem).
; wejście: eax ; wyjście: eax mov edx, eax ; edx = | a | b | c | d | rol edx, 8 ; edx = | b | c | d | a | ror eax, 8 ; eax = | d | a | b | c | and edx, 000ff00ffh ; edx = | 0 | c | 0 | a | and eax, 0ff00ff00h ; eax = | d | 0 | b | 0 | or eax, edx ; eax = | d | c | b | a |
Odpowiedniki rozkazów BSF i BSR
Na procesorze Pentium czas wykonywanie tych rozkazów waha się pomiędzy 7 a 70 cyklami. Przedstawiony poniżej kod wymaga w najgorszym przypadku wykonania 24 prostych instrukcji, w najlepszym 14.
Idea przedstawionego algorytmu jest bardzo prosta, opiera się na wyszukiwaniu binarnym: otóż z każdym krokiem zawężamy przedział poszukiwań, albo inaczej ujmując zwiększamy rozdzielczość algorytmu. Czyli na początku lokalizowany jest najmłodsze słowo zawierające ustawione bity, następnie w tym słowie poszukuję się najmłodszego, niezerowego bajtu, w nim z kolei szuka się najmłodszej niezerowej tetrady itd.
Właściwie wybór jest pomiędzy młodszy/starszy, tak więc rozmiar obiektu zmniejsza się dwukrotnie po każdym kroku algorytmu. Jak łatwo policzyć liczba kroków wynosi log2n, gdzie n to ilość bitów w słowie binarnym.
; implementacja BSF
; wejście: eax
; wyjście: ebx - pozycja pierwszego, ustawionego bitu
soft_bsf:
mov ebx, 2 ; ebx = 2
; zostały pogrubione sprawdzane części dworda
; eax = |0000 0010 0010 0000|**0000 0000 0000 0000**|
test eax, 0x0000ffff ; sprawdź czy w młodszym słowie są
; ustawione jakiekolwiek bity
jnz .skip1 ; jeśli nie, to znaczy, że ustawione bity są
; tylko w starszym słowie
shr eax, 16 ; eax = |0000 0000 0000 0000|0000 0010 **0010 0000**|
add ebx, byte 16 ; ebx = 18
.skip1:
test eax, 0x000000ff ; sprawdź czy w młodszym bajcie są
; ustawione jakiekolwiek bity
jnz .skip2
shr eax, 8
add ebx, byte 8
.skip2:
shr eax, 16 ; eax = |0000 0000 0000 0000|0000 0010 0010 **0000**|
test eax, 0x0000000f ; sprawdź tetrady
jnz .skip3
shr eax, 4 ; eax = |0000 0000 0000 0000|0000 0000 0010 00**10**|
add ebx, byte 4 ; ebx = 22
.skip3:
test eax, 0x00000003 ; sprawdź 2-bitowe pole
jnz .skip4
shr eax, 2
add ebx, byte 2
.skip4:
shr eax, 4 ; eax = |0000 0000 0000 0000|0000 0000 0010 001**0**|
shr al, 1 ; CF = LSB(eax) = 0
sub ebx, 0 ; ebx = 22
ret
Konwersja float na int
Przy użyciu rozkazów FPU konwersja liczby zmiennoprzecinkowej na liczbę całkowitą, dodatkowo uzyskujemy zaokrąglanie zgodne z ustawieniami pola RountControl w rejestrze kontrolnym koprocesora.
fld [float] ; 1 cykl fild [integer] ; 6 cykli
Rozkazy SSE, SSE2 i 3DNow również wspierają konwersje. Przy czym rozkazy SSE mogą to robić dwojako:
- używając funkcji round — dla operacji SSE wprowadzono rejestr MXCSR analogiczny do kontrolnego koprocesora, jest też pole RC, które umożliwia ustawienie sposobu zaokrąglania
- używając funkcji trunc — bez względu na ustawienia pola RC część ułamkowa jest ucinana
Rozkazy z pierwszej grupy zestawiono w tabelce. Dla każdego rozkazu istnieje odpowiednik z grupy drugiej — faktycznie operacje na polach bitowych są identyczne; mnenoniki są prawie takie same, z tą różnicą że dodana została druga literka T, np. CVTTPS2DQ.
CVTPD2DQ xmm1, xmm2/mm128 (double -> dword):
xmm1[31-0] = round(xmm2[63-0]) xmm1[63-32] = round(xmm2[127-64]) xmm1[127-64] = 0``
CVTPS2DQ xmm1, xmm2/mm128 (float -> dword):
xmm1[31-0] = round(xmm2[31-0]) xmm1[63-32] = round(xmm2[63-32]) xmm1[95-64] = round(xmm2[95-64]) xmm1[127-96] = round(xmm2[127-96])
CVTPD2PI mm, xmm/mm128a (double -> dword):
mm[31-0] = round(xmm[63-0]) mm[63-32] = round(xmm[127-64])
CVTPS2PI mm, xmm/mm128 (float -> dword):
mm[31-0] = round(xmm[31-0]) mm[63-32] = round(xmm[63-32])
CVTSD2SI reg32, xmm/mm64 (double -> dword):
reg32[31-0] = round(xmm[63-0])
CVTSS2SI reg32, xmm/mm32 (float -> dword):
reg32[31-0] = round(xmm[31-0])
Przedstawię teraz od kuchni algorytm owej konwersji (ograniczę się do ucinania).
Liczbę floating point opisuje równanie:
( − 1)sign ⋅ (1 + mantissa) ⋅ 2exp + bias
natomiast rozkład bitów w dwusłowie przedstawia się następująco:

Jeśli zostaną wyzerowane bity 23-31 (czyli pola sign i exponent+bias), to wartość dworda (liczona w naturalnym kodzie binarnym) wyniesie mantissa223. Gdy mantysa zostanie uzupełniona, czyli zostanie ustawiony bit 23, to wartość ta wyniesie (1 + mantissa)223. Rozkład bitów poniżej (x oznacza dowolną wartość):
0000 0000 1xxx xxxx xxxx xxxx xxxx xxxx
Pozostaje jeszcze uwzględnić czynniki 2exponent + bias — mnożenie przez potęgę dwójki jest równoważne przesunięciu bitowemu w lewo gdy wykładnik jest dodatni, w prawo gdy jest ujemny; wartość przesunięcia jest oczywiście równa (modułowi) wykładnika, tj. exponent − bias − 23.
Jeśli liczba zostanie przesunięta o więcej niż 24 bity w prawo to jej wartość będzie zawsze równa 0. Z kolei jeśli przesunięcie w lewo przekroczy 7 pozycji to będzie znaczyło, że liczba zmiennoprzecinkowa jest większa od 231, czyli przekracza maksymalną wartość liczby ze znakiem.
Poniżej słowa ubrane zostały w kod (w poprzedniej wersji tego artykułu kod był w asemblerze, niestety nie był w ogóle czytelny).
#include <errno.h>
#include <limits.h>
extern int errno;
typedef unsigned int dword; // 32 bity
const int bias = 127;
typedef union {
struct {
dword mantissa : 23;
dword exp_biased: 8;
dword sign : 1;
} fields;
float value;
} IEEE_float;
int float2int(float value) {
IEEE_float fp;
fp.value = value;
/* d = (1+mantissa)*2^23 */
int d = (1 << 23) | fp.fields.mantissa;
/* exp = exponent */
int exp = (int)fp.fields.exp_biased - bias - 23;
if (exp < -23) /* aba(value) < 1.0 */
return 0;
else
if (exp > 7) { /* abs(value) > 2^30 */
errno = ERANGE;
return (fp.fields.sign) ? INT_MIN : INT_MAX;
}
else {
if (exp > 0)
d <<= exp;
else
d >>= -exp;
return (fp.fields.sign) ? -d : d;
}
}
Obrót punktu 2D (FPU)
Wszystkie obliczenie są wykonywane na liczbach zmiennoprzecinkowych pojedynczej precyzji (4 bajty).
; x' = x*cos(a) - y*sin(a) ; y' = x*sin(a) + y*cos(a) ; ; ca := cos(a) ; sa := sin(a) ; ; st0 st1 st2 st3 st4 st5 fld dword [x] ; x fld dword [a] ; a x fsincos ; ca sa x fld dword [y] ; y ca sa x ; x' fld st0 ; y y ca sa x fmul st3 ; y*sa y ca sa x fld st4 ; x y*sa y ca sa x fmul st3 ; x*ca y*sa y ca sa x fsubrp st1 ; x' y ca sa x ; y' fxch st4 ; y ca sa x x' fmulp st1 ; y*ca sa x x' fxch st2 ; x sa y*ca x' fmulp st1 ; x*sa y*ca x' faddp st1 ; y' x' fstp dword [y] fstp dword [x]
cxchg — Conditional XCHG (x86)
Poniższy kod zamienia dwie liczby, pod warunkiem że najstarszy bit ecx jest ustawiony. Kod jest bez rozgałęzień.
; wejście: eax, ebx
; ecx - "warunek"
;
; MSB(ecx)=1 MSB(ecx)=0
sar ecx, 31 ; ecx=0xffffffff =0x00000000
mov edx, ebx ;
sub edx, eax ;
and edx, ecx ; edx = ebx-eax =0x00000000
add eax, edx ; eax = ebx =eax -- bo, eax+ebx-eax=ebx
sub ebx, edx ; ebx = eax =ebx -- bo, ebx-ebx+eax=eax
nswap — Nibble Swap (x86, MMX)
Zamiana kolejności tetrad
Sposób 1:
; wejście: eax = |hg|fe|dc|ba| ; wyjście: eax = |ab|cd|ef|gh| rol al, 4 ; eax = |hg|fe|dc|ab| rol ah, 4 ; eax = |hg|fe|cd|ab| bswap eax ; eax = |ab|cd|fe|hg| rol al, 4 ; eax = |ab|cd|fe|gh| rol ah, 4 ; eax = |ab|cd|ef|gh|
Sposób 2:
; wejście: eax = |hg|fe|dc|ba| ; wyjście: eax = |ab|cd|ef|gh| ; niszczy: ebx mov ebx, eax and eax, 0x0f0f0f0f ; eax = |0g|0e|0c|0a| and ebx, 0xf0f0f0f0 ; ebx = |h0|f0|d0|b0| shl eax, 4 ; eax = |g0|e0|c0|a0| shr ebx, 4 ; ebx = |0h|0f|0d|0b| or eax, ebx ; eax = |gh|ef|cd|ab| bswap eax ; eax = |ab|cd|ef|gh|
Generacja maski
; wejście: eax
; wyjście: eax -- bajty z ustawionymi MSB mają wartość 0xff, pozostałe 0x00
; niszczy: ebx
; np. 10101101 01110100 11010100 11010101
and eax, 0x80808080 ; eax=10000000|00000000|10000000|10000000
mov ecx, eax
mov ebx, eax ;
shr ebx, 7 ; ebx=00000001|00000000|00000001|00000001|
sub eax, ebx ; eax=01111111|00000000|01111111|01111111|
or eax, ecx ; eax=11111111|00000000|11111111|11111111|
W analogiczny sposób można postąpić przy słowach bitowych nie będących bajtami, np. przy dodawaniu pikseli 15/16bpp.
Mnożenie równoległe (x86)
Jeśli czynniki mnożenia mieszczą się w zakresie bajtu (0...255), to można zastosować taki trik:
; wejście: a,b,c - liczby 0..255 (załóżmy że to stałe) xor eax, eax ; mov al, b ; shl eax, 16 ; mov al, a ; eax = |0|b|0|a| movzx ebx, c mul ebx ; eax = |b*c|a*c|
Wyniki mnożeń nie wypływają na siebie.
Wersja x86 rozkazu paddb
; wejście: eax, ebx - packed bytes mov ecx, eax xor ecx, ebx and eax, 0x7f7f7f7f ; zerowanie MSB and ebx, 0x7f7f7f7f ; add eax, ebx and ecx, 0x80808080 xor eax, ecx
Wersja zoptymalizowana na Pentium:
mov ecx, eax ; 1 and eax, 0x7f7f7f7f ; - xor ecx, ebx ; 2 and ebx, 0x7f7f7f7f ; - add eax, ebx ; 3 and ecx, 0x80808080 ; - xor eax, ecx ; 4
stricmp
Jeśli dwa łańcuchy będą zawierać wyłącznie małe bądź duże litery ASCII, porównanie ich bez względu na rozmiar liter będzie bardzo proste.
; edi - łańcuch A
; esi - łańcuch B
; eax - wynik zgodny z konwencją stricmp
stricmp:
.compare:
mov al, [edi]
mov ah, [esi]
or al, al ; znak '\0'?
jz .end
or ah, ah ; znak '\0'?
jz .end
xor al, ah ; litery mogą różnić się
; co najwyżej 5 bitem
test al, 0xdf ; jeśli różnią się jakimś innym bitem
jz .end ; kończ
inc edi
inc esi
jmp .compare
.end:
movzx ebx, [edi]
movzx eax, [esi]
sub eax, ebx
ret
Population Count
x86 — naiwne podejście
Obliczenie ilości ustawionych bitów w dwusłowie.
; ebx - argument
; eax - wynik
popcount:
mov eax, 0
mov ah, 32 ; ilość bitów
.count:
rol ebx, 1
adc al, 0
loop .count
movzx eax, al
ret
rozkazy SSSE3 oraz tablice
Zobacz w osobnym artykule.
Implementacja funkcji modf() (FPU)
Funkcja modf rozbija liczbę zmiennoprzecinkową na część ułamkową i całkowitą.
; wejście:
; st0 - x
; wyjście:
; st0 - floor(x)
; st1 - fract(x)
_modf:
; st0 st1 st2
; x
fld1 ; 1 x
fld st1 ; x 1 x
fprem ; fract(x) 1 x
fxch st2 ; x 1 fract(x)
fsub st2 ; floor(x) 1 fract(x)
fxch ; 1 floor(x) fract(x)
fcomp st1 ; floor(x) fract(x)
ret
Wykorzystano fakt, że fprem wykonuje operację st0 := st0 - floor(st0/st1)*st1.
Jeśli koprocesor jest ustawiony w tryb ucinania (ang. truncate), tj. pole RC słowa kontrolnego zawiera wartość 11b to można użyć alternatywnego kodu.
_modf:
; st0 st1 st2
; x
fld st0 ; x x
frndint ; floor(x) x
fsub st1, st0 ; floor(x) x-floor(x)=
fract(x)
ret
; al: 00b - round to nearest
; 01b - round down
; 10b - round up
; 11b - round toward zero
;
; RC_temp dw ?
setRCfield:
fstcw [RC_temp]
and ax, 11b
shl ax, 10 ; pole RC zajmuje bity 10 i 11
and word [RC_temp], 0xf3ff
or word [RC_temp], ax
fldcw [RC_temp]
ret
Implementacja funkcji pow(x, y) (FPU)
Użyjemy tożsamości xy = 2ylog2(x).
Rozkaz fly2x oblicza wartość wyrażenia ylog2x (ozn. W). Obliczania potęg dwójki realizuje rozkaz f2xm1: (2x − 1), jednak argumentem mogą być wyłącznie liczby z przedziału ( − 1, + 1).
Skorzystajmy zatem z kolejnej tożsamości: 2a + b = 2a ⋅ 2b, przy czym a = floor(W) i b = fract(W).
; wejście
; st0 - x
; st1 - y
; wyjście:
; x^y
power:
; st0 st1 st2 ... st7
; x y
fyl2x ; W
fld1 ; 1 W
fld st1 ; W 1 W
fprem ; fract(W) 1 W
f2xm1 ; 2^fract(W)-1 1 W
fadd st1 ; 2^fract(W) 1 W
fincstp ; 1 W 2^fract(W)
fscale ; 2^floor(W) W
fdecstp ; 2^fract(W) 2^floor(W) W
fmulp st1 ; 2^W W
ffree st1 ; 2^W
ret
Przypomnę tylko, że rozkaz fscale wykonuje następującą operację st0.wykładnik += floor(st1).
min/max (cmov)
; min ; eax, ebx - argumenty ; eax - wynik ; if (a < b) a = b cmp eax, ebx cmovl eax, ebx ; lub cmovb dla liczb bez znaku
Implementacja funkcji intpow(double, int)
Obliczenie potęgi z wykładnikiem będącym potęgą dwójki (x2k) wymaga zaledwie k mnożeń:
while (k--)
x *= x;
Z kolei każdą liczbę można reprezentować jako sumę potęg dwójki (system binarny). Korzystając z własności pokazanej wyżej, oraz ze wzoru na iloczyn potęg o tych samych podstawach można zapisać następujący algorytm:
double intpow(double x, unsigned int exponent)
{
double result = 1.0;
for (bit=0; bit<k; bit++)
{
if (bitset(exponent, bit))
result *= x;
x *= x; // obliczenie x^(2^(i+1))
}
return result;
}
Koszt stały algorytmu to k mnożeń, w zależności od ilości ustawionych bitów wykładnika może wykonać się od 0 do k dodatkowych mnożeń. Liczba k to pozycja najstarszego ustawionego bitu wykładnika.
; wejście:
; st0 - x
; eax - wykładnik (liczba bez znaku!)
; wyjście
; st0 - x^eax
intpow:
; st0 st1
; x
fld1 ; 0 x
fxch ; x 1
.loop:
test eax, eax
jz .endloop
shr eax, 1
jnc .skip ; if (bitset(exponent, bit))
fmul st1, st0 ; result *= x;
.skip:
fmul st0, st0 ; x *= x;
jmp .loop
.endloop:
; st0 st1
; x^k x^eax
fcomp ; x^eax
Wyświetlanie liczb floating-point (FPU)
Rozkaz fbstp zapisuje część całkowitą st0 jako liczbę BCD (spakowaną). Część całkowita jest uzyskiwana poprzez zaokrąglenie st0 zgodnie z metodą ustawioną w polu RC. Zapisywanych jest maksymalnie 18 cyfr (9 bajtów), w dodatkowym bajcie zapisywany jest znak.
; wejście:
; esi - adres 10-bajtowego bufora na liczby BCD
; edi - adres 19-bajtowego bufora na zapis ASCII (znak+18 cyfr)
; st0 - konwertowana liczba
float_convert:
pushad
fbstp [esi] ; konwertowany element jest usuwany ze stosu
add esi, byte 8 ; zaczynamy od końca łańcucha BCD
mov al, [esi+1] ; if ((al=[esi + 1]) & 0x80)
test al, 0x80 ; [edi++] = byte('+');
jnz .plus ; else
.minus: ; [edi++] = byte('+');
mov [edi], byte '-' ;
jmp .endif ;
.plus: ;
mov [edi], byte '+' ;
.endif: ;
inc edi ;
mov ecx, 9
.unpackBCD:
movzx ax, byte [edi] ; al := [edi--], ah := 0
dec edi ;
; ax = |0|0|B|A|
rol al, 4 ; ax = |0|0|A|B|
shl ax, 4 ; ax = |0|A|B|0| -- zamiast tych dwu rozkazów (shl, shr)
shr al, 4 ; ax = |0|A|0|B| -- można użyć rozkazu 'aam 16' (db 0xd4,0x10)
add ax, 0x3030 ; konwersja na ASCII
mov [edi], ax ; zapisanie dwóch znaków
add edi , byte 2 ; do łańcucha
loop .unpackBCD
popad
ret
Rozkaz fbstp zapisuje wszystkie cyfry, także zera nieznaczące, należy usunąć je samodzielnie:
; edi -> łańcuch ASCII
syscall WRITE, stdout, edi, 1 ; wyświetl znak
inc edi
mov ecx, 17
.skip_leading_zeros: ; ecx = 17
mov al, [edi] ; while ([edi] == '0') edi++, ecx--;
cmp al, '0' ;
jne .end ; write(stdout, edi, ecx+1)
inc edi
dec ecx
jz .end
jmp .skip_leading_zeros
.end:
inc ecx
; tutaj "jakoś" zapisujemy znak na wyjście
syscall WRITE, stdout, edi, ecx
Extract Bit String
Funkcja wyciąga ciąg bitów z qworda, podawany jest początek ciągu i jego długość. Funkcja została przesłana na grupę pl.comp.programming.
; wejście:
; cl - pozycja ciągu (0..31)
; ch - długość ciągu bitów (0..31)
; esi - adres qworda
; wyjście:
; eax - wartość (ze znakiem)
extract_signed:
; np. cl = 26
; ch = 11
mov eax, [esi+0] ; eax = |abcd ef00|0000 0000|0000 0000|0000 0000|
mov ebx, [esi+4] ; ebx = |0000 0000|0000 0000|0000 0000|000A BCDE|
shrd eax, ebx, cl ; eax = |0000 0000|0000 0000|0000 0ABC|DEab edef|
mov cl, 32 ; cl = 32-ch
sub cl, ch
shl eax, cl ; eax = |ABCD Eabe|def0 0000|0000 0000|0000 0000|
sar eax, cl ; eax = |AAAA AAAA|AAAA AAAA|AAAA AABC|DEab edef| -- 'shl' dla unsigned
ret
Mnożenie wektora 4x1 przez macierz 4x4 (FPU)
Macierz M zawiera przekształcenia geometryczne, przemnożenie jej przez wektor V spowoduje przekształcenie wektora. Macierz może być column-majority lub row-majority — w zależności od tego wektor jest mnożony prawo- lub lewostronnie.
Na rysunku przedstawiono macierz row-majority, czyli takiej gdzie mnożone są wiersze:
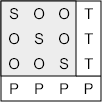
- s — informacja o skalowaniu*
- o — informacja o obrotach i pochylaniu
- T — wektor translacji
- P — informacja o perspektywie
* — zaznaczony na szaro minor 3x3 to de facto skumulowana informacja o skalowaniu, obrocie i pochyleniu.
Przy mnożeniu macierzy, tak naprawdę, liczone są iloczyny skalarne (ang. dot product) wiersza (w przypadku row-majority) z wektorem. Stałym argumentem funkcji dot_product jest wektor V, optymalizacja polega na tym, by współrzędne wektora były ładowane jednokrotnie na stos koprocesora.
; 10-08-01
%define offset
x equ 0
y equ 4
z equ 8
w equ 12
mov si, offset matrix
mov di, offset vector_out
mov cl, 4
; st0 st1 st2 st3 st4 st5
fld dword [vector_in+w] ; w
fld dword [vector_in+z] ; z w
fld dword [vector_in+y] ; y z w
fld dword [vector_in+x] ; x y z w
.loop: ; zmiana zawartości stosu koprocesora przy
; jednym mnożeniu skalarnym
fld st0 ; x x y z w
fmul dword [si] ; ax x y z w
fld st2 ; y ax x y z w
fmul dword [si+4] ; by ax x y z w
faddp st1 ; ax+by x y z w
fld st3 ; z ax+by x y z w
fmul dword [si+8] ; cz ax+by x y z w
faddp st1 ;ax+by+cz x y z w
fld st4 ; w abc x y z w
fmul dword [si+12] ; dw abc x y z w
faddp st1 ; abc+dw x y z w
; [di] <- ax+by+cz+dw
fstp dword [di] ; x y z w
add di, 4 ; następna współrzędna z 'vector_out'
add si, 4*4 ; następny wiersz w macierzy 'matrix'
dec cl ; pętla
jnz .loop ; /
fcompp ; y w
fcompp ; wszystkie rej. FPU są puste
x86: równoległe tworzenie maski dla niezerowych bajtów (5.07.2007)
Specyfikacja dla jednego bajtu:
mask = (x != 0) ? 0xff | 0x00
(Działanie analogiczne do MMX-owych funkcji pcmpXX).
Metoda:
-- x - argument (bajt)
a = x & 0x80 -- najstarszy bit
b = x & 0x7f -- 7 młodszych bitów
c = b + 0x7f -- najstarszy bit =1, gdy którykolwiek
bit b był ustawiony
d = (c | a) & 0x80 -- najstarszy bit =1, gdy x != 0
mask = d | (d - (d >> 7))
Kod x86:
; eax - wektor 4 bajtów movl %eax, %ebx andl $0x80808080, %ebx ; ebx = a andl $0x7f7f7f7f, %eax ; eax = b addl $0x7f7f7f7f, %eax ; eax = c orl %ebx, %eax andl $0x80808080, %eax ; eax = d movl %eax, %ebx ; ebx = d (zapisane) movl %eax, %ecx ; ecx = d shrl $7, %ebx ; ebx = d >> 7 subl %ebx, %eax ; eax = d - (d >> 7) orl %ecx, %eax ; eax = d | (d - (d >> 7))
Tworzenie maski z ustawionymi/wyzerowanymi bitami na młodszych pozycjach (19.08.2007)
Maska jest postaci: a) 1111110000000000 lub b) 0000111111111111, gdzie parametrem jest pozycja pierwszego zgaszonego/zapalonego bitu liczona od zera.
Maskę a) można utworzyć w następujący sposób:
; eax - pozycja bitu
; edx - maska
; eax = 17
xor %edx, %edx ; 00000000 00000000 00000000 00000000 <- LSB
bts %eax, %edx ; 00000000 00000010 00000000 00000000
dec %edx ; 00000000 00000001 11111111 11111111
natomiast b) tak:
; eax - pozycja bitu
; edx - maska
; eax = 17
mov $-1, %edx ; 11111111 11111111 11111111 11111111 <- LSB
bts %eax, %edx ; 11111111 11111101 11111111 11111111
inc %edx ; 11111111 11111110 00000000 00000000