Punkty przecięcia dwóch krzywych Beziera 3. stopnia

Autor:	Wojciech Muła
Dodany:	15.02.2007

Analitycznie jest to możliwe: jedną z krzywych wyraża się za pomocą funkcji uwikłanej f(x, y) = 0 (wykonalne), a funkcje tworzące drugą krzywą podstawia (wykonalne) i otrzymujemy wielomian 9. stopnia ze względu na parametr drugiej krzywej. Praktyczny problem to wyznaczenie pierwiastków wielomianu.

Dlatego o wiele prościej aproksymować dwie krzywe łamaną — krzywe są dzielone na coraz mniejsze łuki aż do chwili, gdy staną się dostatecznie „płaskie” (zobacz w osobnym artykule), a wtedy zastąpić je odcinkami i obliczyć przecięcia, co jest bardzo łatwe. Jeśli krzywe zostaną podzielone na dostatecznie krótkie łuki, można odczytać punkty przecięcia i wartości parametrów z praktycznie dowolną dokładnością.

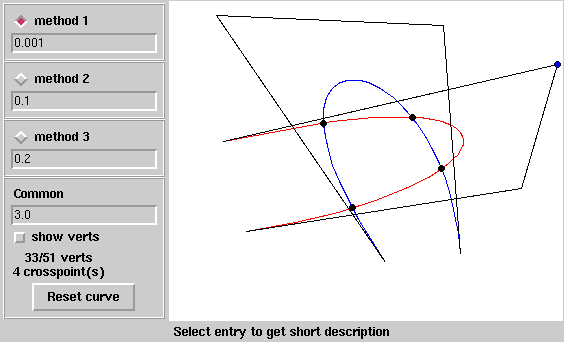
Program:

• cbezier-cc-tkdemo.py

Wymaga:

• cbezier2D.py — różne funkcje dotyczące krzywych Beziera 3. stopnia, w tym cc_intersection realizująca wyznaczanie punktów przecięć
• aabb2D.py — pudełka otaczające w 2D,
• utils2D.py — działania na wektorach (pary (x, y)),
• poly_root.py — pierwiastki wielomianów 1., 2. i 3. stopnia.