Stwierdzenie, czy krzywa Beziera 3. stopnia jest płaska
| Autor: | Wojciech Muła |
|---|---|
| Dodany: | 30.01.2007 |
| Zmodyfikowany: | 7.02.2007 |
Gdzie jest to potrzebne? Przy aproksymacji (przybliżaniu) krzywej za pomocą łamanej, co ma z kolei zastosowanie przy:
- rysowaniu krzywych,
- wyznaczaniu długości łuku (niewykonalne analitycznie),
- wyznaczanie przecięcia krzywych.
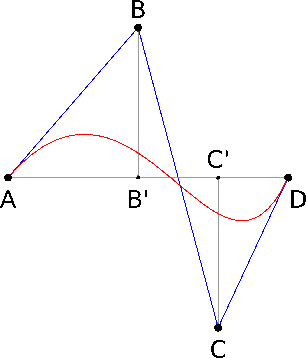
Sposoby określania „płaskości”
Krzywa jest tym bardziej „płaska” im przechodzi bliżej odcinka AD.
Sposób 1.
Jeśli długość łamanej kontrolnej jest porównywalna z długością odcinka AD, tj. (|AB| + |BC| + |CD|)/|AD| = 1 + eps, gdzie eps jest bardzo małą liczbą, mniejszą od 1 (w praktyce znacząca cyfra pojawia się kilka miejsc po przecinku)
Wada: spore koszty obliczeniowe (4 długości odcinków, dzielenie)
Sposób 2.
Sposób jest uproszczeniem 3., mianowicie zakłada się, że B = 1/3 ⋅ A + 2/3 ⋅ D i 2/3 ⋅ A + 1/3 ⋅ D, a więc punkty kontrolne B i C są rozmieszczone równomiernie na odcinku AD.
Co więcej w idealnym przypadku zachodzi: B = (A + C)/2 oraz C = (B + D)/2 (mały nakład obliczeniowy) — wystarczy stwierdzić jak daleko od tych idealnych pozycji znajdują się rzeczywiste punkty B i C.
Odległość nie musi być mierzona metryką euklidesową (pominięcie czasochłonnego pierwiastkowania), wystarczy metryka Manhattan, o wiele szybsza do wyznaczenia.
Sposób 3.
Jeśli punkty kontrolne A, B, C, D są współliniowe, wówczas krzywa jest płaska (ale niekoniecznie redukuje się do odcinka!). Jest tak wówczas, gdy długość odcinków |BB'| i |CC'| jest mała w stosunku do |AD| oraz rzuty B' oraz C' leżą na odcinku AD.