Drawing trees

Author:	Wojciech Muła
Added on:	2025-01-12

Problem

We have a tree of any degree and depth. Each node has assigned a bounding box of its graphical representation.

We want to draw such data structure, taking into account geometry of nodes.

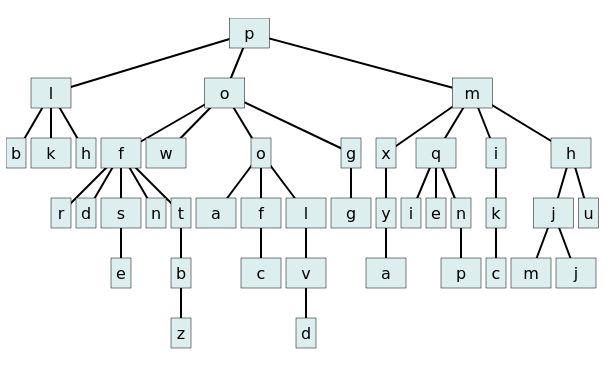
Algorithm

The algorithm to draw trees runs in two phases. In the first phase we group nodes by their depths. For each depth we calculate the maximum height and assign nodes at y coordinate. The y value is the sum of height of previous depths plus some horizontal spacing between each level.

The second phase places horizontally the nodes at the given depth. We scan nodes by their depths, starting from the deepest level, up to the root; nodes are scanned left-to-right.

The current node is moved to the right border of its predecessor, with some horizontal space, like node.x = prev.x + prev.width + x_space. Then, we calculate the x coordinate of node center: x_c = node.x + node.width/2.

If the node has children, we calculate the desired x coordinate x_d. It may be simply an average of the first and last child centers, visually better results are obtained by averaging centers of all children nodes.

When x_d > x_c, we move only the current node right by dx = x_d − x_c (its siblings on the right are undefined).


                  xc              xd
                   │               |
                   ▼               │
       ╶──────┐ ┌──────┐           │
depth         │ │ node │           │
       ╶──────┘ └──────┘           │
                                   ▼
                ┌─────────┐ ┌─────────┐ ┌─────────┐
depth + 1       │ child 0 │ │ child 1 │ │ child 2 │
                └─────────┘ └─────────┘ └─────────┘


                                  xd
                                   │
                                   ▼
       ╶──────┐                ┌──────┐
depth         │                │ node │
       ╶──────┘                └──────┘

                ┌─────────┐ ┌─────────┐ ┌─────────┐
depth + 1       │ child 0 │ │ child 1 │ │ child 2 │
                └─────────┘ └─────────┘ └─────────┘

When x_d < x_c, we move to the right all subtress rooted on children nodes of: 1) the current node and 2) all its siblings to the right. We cannot move the deeper nodes to the left, as we assume these nodes are already correctly placed. On the other hand, there are not constraints to the right.


                                       xc
                                       │
                                       ▼
             ┌────────────┐ ┌─────┐ ┌──────┐
depth        │            │ │     │ │ node │
             └────────────┘ └─────┘ └──────┘

             ╶────┐ ┌─────────┐ ┌─────────┐
depth + 1         │ │ child 0 │ │ child 1 │
             ╶────┘ └─────────┘ └─────────┘
                               ▲
                               │
                               xd


                                       xc
                                       │
                                       ▼
             ┌────────────┐ ┌─────┐ ┌──────┐
depth        │            │ │     │ │ node │
             └────────────┘ └─────┘ └──────┘

             ╶────┐         ┌─────────┐ ┌─────────┐
depth + 1         │         │ child 0 │ │ child 1 │
             ╶────┘         └─────────┘ └─────────┘
                                       ▲
                                       │
                                      xd

Live demo

Try algorithm on-line.