AVX512VBMI — remove spaces from text

Author:	Wojciech Muła
Added on:	2019-01-05
Updated on:	2019-01-13 (added Zach Wegner implementation, compare with fast AVX2 code by Michael Howard)

Contents

Introduction
Scalar code
SSE solution
AVX512VBMI solution
- Algorithm outline
- Implementation
PEXT-based algorithm
AVX512VBMI2 algorithm
AVX512VBMI evaluation
Acknowledgements
See also
Source code

Introduction

Removing spaces from a string is a common task in text processing. Instead of removing single character we often want to remove all the white space characters or the punctuation characters etc.

In this article I show an AVX512VBMI implementation. The algorithm is not faster than the scalar code for all cases. But for many it can be significantly faster, and what is more important, in tests on real-world texts it performs better.

Update 2019-01-13: this article pop up on twitter and Hacker News where provoked an incredibly fruitful discussion. Travis Downs noticed that branch mispredictions can be compensated by unrolling the loop in the initial algorithm. Zach Wegner came up with an algorithm which works in constant time by using PEXT instruction. Michael Howard shared with his scalar and AVX2 variants of "despacing" procedure. I'd like to thank all people discussed this topic both on HN and twitter.

Scalar code

A scalar code which does this task is really simple:

char* remove_spaces__scalar(const char* src, char* dst, size_t n) {
    for (size_t i=0; i < n; i++) {
        if (src[i] == ' ' || src[i] == '\r' || src[i] == '\n')
            continue;

        *dst++ = src[i];
    }

    return dst;
}

The function returns the pointer to last written character. This implementation work correctly also for an in-place scenario, i.e. when src and dst point the same memory area.

SSE solution

In SSE code we process 16 bytes of input text. We determine a byte-mask for characters that must be removed — usually with a comparison:

// indices      0   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15

// input    = ['a'|' '|'c'|'a'|'t'|' '|'p'|'l'|'a'|'y'|'s'|' '|'w'|'i'|'t'|'h']
// bytemask = [ 00| ff| 00| 00| 00| ff| 00| 00| 00| 00| 00| ff| 00| 00| 00| 00]
__m128i bytemask = _mm_cmpeq_epi8(input, _mm_set1_epi8(' '));

This mask is converted into a 16-bit number using instruction PMOVMSKB (intrinsic function _mm_movemask_epi8). The number is used to fetch a byte pattern from a precompiled set, which is the argument to PSHUFB (_mm_shuffle_epi8). The shuffle instruction allows to change order of bytes in an SSE register — in our case it skip all spaces.

// input    = ['a'|' '|'c'|'a'|'t'|' '|'p'|'l'|'a'|'y'|'s'|' '|'w'|'i'|'t'|'h']
// shuffle  = [ 0 | 2 | 3 | 4 | 6 | 7 | 8 | 9 | 10| 12| 13| 14| 15| -1| -1| -1]
const uint16_t mask   = _mm_movemask_epi8(bytemask);
const __m128i shuffle = lookup_table[mask];

// output   = ['a'|'c'|'a'|'t'|'p'|'l'|'a'|'y'|'s'|'w'|'i'|'t'|'h'| 0 | 0 | 0 ]
const __m128i output  = _mm_shuffle_epi8(input, shuffle);

// write all 16 bytes
_mm_store_si128((__m128i*)(dst), output);
dst += 16 - popcnt(mask);

Please note that in the example the last three indices are -1 and bytes past compressed characters are zeros. In practise it doesn't matter what will be there.

A clear drawback of the SSE solution is a huge lookup table. It has 65536 entries, each entry occupies 16 bytes, thus all data has exactly 1MB.

AVX512VBMI solution

AVX512 operates on 64-byte register. The extension AVX512VBMI introduced instruction VPERMB (_mm512_permutexvar_epi32) which similarly to PSHUFB can change order of bytes within an AVX512 register. For readers who are not familiar with AVX512 nuances, the extension AVX512BW also defines a byte shuffling instruction, but it operates on the register lanes (16-byte subvectors) not the whole register.

Since AVX512 registers are so wide, use of a lookup table to fetch shuffle patterns is simply impossible. Such table would occupy 2⁷⁰ bytes (2⁴⁰ is 1TB).

Instead of precalculating shuffle patterns, I propose to build them in runtime. This might seem not optimal on the first sight, but the evaluation shows that it's not that bad.

Algorithm outline

In AVX512 code we process 64-byte block. From the input vector we obtain a 64-bit mask for spaces, and then modify the shuffle vector using this mask.

Initially the shuffle vector defines identity transformation, i.e. if applied to the shuffle instruction it would copy all i-th input bytes onto i-th output byte. Technically, the vector contains sequence of bytes from 0 to 63.

Single whitspace

Let's assume there's exactly one space in the input vector, say at the position 5; this will be our building block for the rest of algorithm.

The shuffle vector:

shuffle = [0, 1, 2, 3, 4, 5, 6, 7, 8, ...]
                          ^

must become:

shuffle = [0, 1, 2, 3, 4, 6, 7, 8, 9, ...]

In other words we must perform following vector addition:

[0, 1, 2, 3, 4, 5, 6, 7, 8, ...]  +
[0, 0, 0, 0, 0, 1, 1, 1, 1, ...]

To do this we use a nice AVX512 facility, the masked add.

const __m512i = _mm512_set1_epi8(1);
const uint64_t addmask = /* ??? */

shuffle = _mm512_mask_add_epi8(shuffle, addmask, shuffle, ones);

But how to cheaply calculate a proper mask? From mask 000...000100000, we have to get 111...111100000, i.e. all bits above the set bit must also be ones. The input mask has exactly one bit set; we subtract 1:

000...00100000 - 1 = 000...000011111

Now all bits below become 1, thus a bit negation yields the required bit pattern. The full expression in C is like this:

const uint64_t addmask = ~(mask - 1);

More isolated whitspaces

Now let's consider a more complex case. The input vector contains two non-adjacent spaces. Assume the first one is at index 2, and the second one at 5, thus the bit mask is 000...000100100.

First we isolate the lowest bit set using expression (x & -x), or x & (~x + 1); on an AVX512VBMI CPU this expression should be compiled into single instruction BLSI:

// mask  = 000...00000100100
// first = 000...00000000100

uint64_t first = (mask & -mask);

Since the mask first has exactly one bit set, we use the procedure described in the previous section to modify the shuffle pattern:

shuffle = [0, 1, 2, 3, 4, 5, 6, 7, 8, ...]
        + [0, 0, 1, 1, 1, 1, 1, 1, 1, ...]
        = [0, 1, 3, 4, 5, 6, 7, 8, 9, ...]

Now, we reset the first bit set from mask:

// mask  = 000...00000100100
//       ^ 000...00000000100
//       = 000...00000100000
mask = mask ^ first;

And we can again extract the lowest bit set. Hold on, can we? No, it's not possible as the shuffle pattern has just been changed, thus our initial 5th bit doesn't indicate the space character. Since one character was skipped, the another space character is at index 4.

To reflect this change the mask must be shifted right by 1:

mask >>= 1;

Now, we might safely extract the lowest bit set and modify the shuffle pattern:

shuffle = [0, 1, 3, 4, 5, 6, 7, 8, 9, ...]
        + [0, 0, 0, 0, 1, 1, 1, 1, 1, ...]
        = [0, 1, 3, 4, 6, 7, 8, 9, 10, ...]

Obviously, if there are more ones in the mask, we need to carry on the above procedure (extract bit, reset, shift). If mask becomes zero we stop modifying the shuffle vector.

Runs of whitespaces

There's still one problem to solve, what if there are more spaces in a row. For instance, the run has three ones starts at index 2: 000...00011100.

We need to modify shuffle vector starting from index 2, but increment is 3 not 1:

shuffle = [0, 1, 2, 3, 4, 5, 6, 7, 8, ...]
        + [0, 0, 3, 3, 3, 3, 3, 3, 3, ...]
        = [0, 1, 5, 6, 7, 8, 9, 10, 11, ...]

Firstly, we must save the position (mask) for the first bit of run. Then we need detect if the next set bit (a) continues the run, or (b) starts a new one. If it's a continuation, we increment by one a vector that holds run's length. If it's a new run, the shuffle vector is modified with length vector.

uint64_t first;
uint64_t curr;

__m128i increment = ones;

first = (mask & -mask);
mask  = (mask ^ first) >> 1;

while (/* some condition*/) {
    curr = (mask & -mask);
    mask = (mask ^ curr) >> 1;
    if (/* run continues */)
        increment = _mm512_add_epi8(increment, ones);
    else {
        /* finalize the previous run */
        shuffle = _mm512_mask_add_epi8(shuffle, ~(first - 1), shuffle, increment);

        /* initialize a new one */
        first = curr
        increment = ones;
    }
}

How to detect the continuation? We need to keep the previously extracted mask, if it's equal to the currently extracted mask, it's a continuation. Equality works because after each extraction the mask is shifted.

Below is sequence of values which appear during analysing the second bit of a run; as we see the mask curr is equal to prev.

// mask = 000...00011100
// prev = 000...00000100
prev = (mask & -mask)
// mask = 000...00001100
mask = (mask ^ curr) >> 1;
// curr = 000...00000100
curr = (mask & -mask);

Implementation

Below is an actual AVX512VBMI code which implements all the techniques presented above.

char* remove_spaces__avx512vbmi(const char* src, char* dst, size_t n) {

    assert(n % 64 == 0);

    // values 0..63
    const __m512i no_gaps_indices = _mm512_setr_epi32(
        0x03020100, 0x07060504, 0x0b0a0908, 0x0f0e0d0c,
        0x13121110, 0x17161514, 0x1b1a1918, 0x1f1e1d1c,
        0x23222120, 0x27262524, 0x2b2a2928, 0x2f2e2d2c,
        0x33323130, 0x37363534, 0x3b3a3938, 0x3f3e3d3c
    );

    const __m512i ones   = _mm512_set1_epi8(1);
    const __m512i NL     = _mm512_set1_epi8('\n');
    const __m512i CR     = _mm512_set1_epi8('\r');
    const __m512i spaces = _mm512_set1_epi8(' ');

    size_t len;
    for (size_t i=0; i < n; i += 64) {

        const __m512i input  = _mm512_loadu_si512((const __m512i*)(src + i));
        __m512i output;

        uint64_t mask = _mm512_cmpeq_epi8_mask(input, spaces)
                      | _mm512_cmpeq_epi8_mask(input, NL)
                      | _mm512_cmpeq_epi8_mask(input, CR);

        if (mask) {
            len = 64 - __builtin_popcountll(mask);
            __m512i indices = no_gaps_indices;
            __m512i increment = ones;

            uint64_t first;
            uint64_t prev;

            first = (mask & -mask);
            prev  = first;
            mask ^= first;
            mask >>= 1;

            while (mask) {
                const uint64_t curr = (mask & -mask);
                mask ^= curr;
                mask >>= 1;

                if (prev == curr) {
                    increment = _mm512_add_epi8(increment, ones);
                    prev = curr;
                } else {
                    indices = _mm512_mask_add_epi8(indices, ~(first - 1), indices, increment);

                    first = curr;
                    prev  = curr;
                    increment = ones;
                }
            }

            indices = _mm512_mask_add_epi8(indices, ~(first - 1), indices, increment);

            output = _mm512_permutexvar_epi8(indices, input);
        } else {
            output = input;
            len = 64;
        }

        _mm512_storeu_si512((__m512i*)(dst), output);
        dst += len;
    }

    return dst;
}

PEXT-based algorithm

Zach Wegner proposed to utilize instruction PEXT (_pext_u64) which does compression of bits based on given mask. Suppose we have a binary value:

v = 0011_1111_0111_0101

and mask of whitespace characters:

m = 0100_0001_0110_1000

PEXT(v, m) yields:

0011_1111_0111_0101
0100_0001_0110_1000
 0      1  11  0     -> 0000_0000_0000_1110
                                     ^ ^^^^
                              bits extracted from v

The idea is to compress in this way individual bits of indices ("layers") and then rebuild numeric values from these bits. Let's start with an example for 4-bit indices:

input           = ['a'|' '|'c'|'a'|'t'|' '|'p'|'l'|'a'|'y'|'s'|' '|'w'|'i'|'t'|'h']
index           =   0   1   2   3   4   5   6   7   8   9  10   11  12  13  14  15
whitespace mask =   0   1   0   0   0   1   0   0   0   0   0   1   0   0   0   0  = 0x0822

bits #0 of index    0   1   0   1   0   1   0   1   0   1   0   1   0   1   0   1  = 0x5555
bits #1 of index    0   0   1   1   0   0   1   1   0   0   1   1   0   0   1   1  = 0xcccc
bits #2 of index    0   0   0   0   1   1   1   1   0   0   0   0   1   1   1   1  = 0xf0f0
bits #3 of index    0   0   0   0   0   0   0   0   1   1   1   1   1   1   1   1  = 0xff00

Each bit "layer" is then compressed with PEXT according to negation of whitespace mask:

mask = ~0x0822 = 0xf7dd;

b0 = _pext_u64(0x5555, mask) = 0b1_0100_1010_0100 = 0x14a4
b1 = _pext_u64(0xcccc, mask) = 0b1_1001_0011_0110 = 0x1936
b2 = _pext_u64(0xf0f0, mask) = 0b1_1110_0011_1000 = 0x1e38
b3 = _pext_u64(0xff00, mask) = 0b1_1111_1100_0000 = 0x1fc0

The last step is reconstruction of index values from individual bits. This is done by masked add of bit weights, which are 1, 2, 4, 8, 16, 32 etc.

Below is an actual implementation. Please just note that in case of AVX512 indices are 6-bit numbers.

char* remove_spaces__avx512vbmi__zach(const char* src, char* dst, size_t n) {
    assert(n % 64 == 0);

    const __m512i NL     = _mm512_set1_epi8('\n');
    const __m512i CR     = _mm512_set1_epi8('\r');
    const __m512i spaces = _mm512_set1_epi8(' ');

    uint64_t index_masks[6] = {
        0xaaaaaaaaaaaaaaaa,
        0xcccccccccccccccc,
        0xf0f0f0f0f0f0f0f0,
        0xff00ff00ff00ff00,
        0xffff0000ffff0000,
        0xffffffff00000000,
    };

    const __m512i index_bits[6] = {
        _mm512_set1_epi8(1),
        _mm512_set1_epi8(2),
        _mm512_set1_epi8(4),
        _mm512_set1_epi8(8),
        _mm512_set1_epi8(16),
        _mm512_set1_epi8(32),
    };

    size_t len;
    for (size_t i=0; i < n; i += 64) {
        const __m512i input  = _mm512_loadu_si512((const __m512i*)(src + i));
        __m512i output;

        uint64_t mask = _mm512_cmpeq_epi8_mask(input, spaces)
                      | _mm512_cmpeq_epi8_mask(input, NL)
                      | _mm512_cmpeq_epi8_mask(input, CR);

        if (mask) {
            len = 64 - __builtin_popcountll(mask);
            mask = ~mask;
            __m512i indices = _mm512_set1_epi8(0);
            for (size_t index = 0; index < 6; index++) {
                uint64_t m = _pext_u64(index_masks[index], mask);
                indices = _mm512_mask_add_epi8(indices, m, indices, index_bits[index]);
            }

            output = _mm512_permutexvar_epi8(indices, input);
        } else {
            output = input;
            len = 64;
        }

        _mm512_storeu_si512((__m512i*)(dst), output);
        dst += len;
    }

    return dst;
}

AVX512VBMI2 algorithm

The extension AVX512VBMI2 defines instruction VPCOMPRESSB (_mm512_mask_compress_epi8) that performs the operation we just programmed.

AVX512VBMI evaluation

The AVX512VBMI code shown above was compared with the scalar implementation.

CPU: Intel(R) Core(TM) i3-8121U CPU @ 2.20GHz

GCC: 7.3.1 20180303 (Red Hat 7.3.1-5)

name	comments
scalar	a naive implementation
AVX512VBMI	input-sensitive implementation with unrolling as suggested by Travis Downs
AVX512VBMI-pext	Zach Wegners' implementation
AVX2	a vector implementation provided by Michael Howard, which calculates prefixed sum without use any precalculated tables (procedure `despace_avx2_vpermd`); it's a very neat procedure

Microbenchmark

Microbenchmark tests removing spaces in a 64-byte block.

Number of spaces in a block varies from 1 to 64. There were 10 random patterns, and for each patter a tested procedure was executed 10.000 times.

The microbenchmark reports two pairs of measurements (in CPU cycles/input byte):

10 times: average number over 10.000 runs;
10 times: the best time.

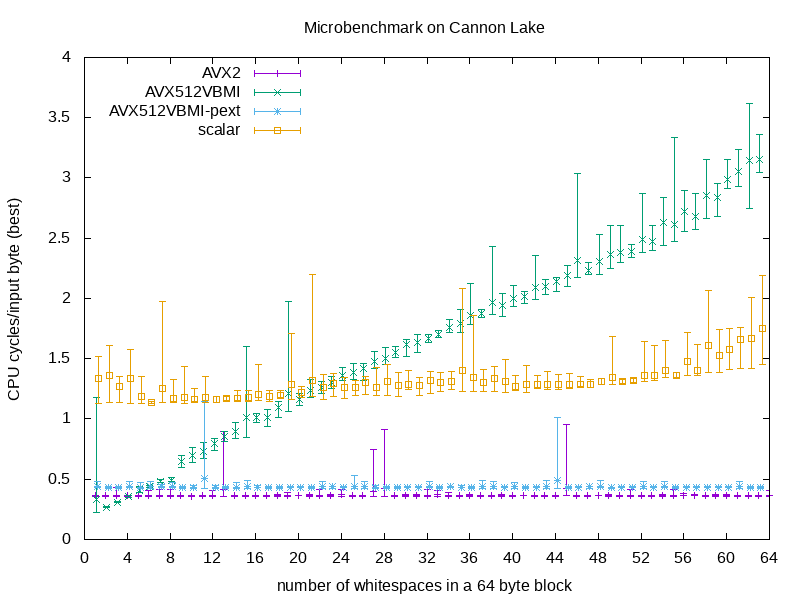
number of spaces	scalar [cycles/byte]			AVX512VBMI [cycles/byte]			AVX512VBMI-pext [cycles/byte]			AVX2 [cycles/byte]
	avg (min)	avg (max)	best	avg (min)	avg (max)	best	avg (min)	avg (max)	best	avg (min)	avg (max)	best
1	1.129	1.517	1.062	0.227	1.178	0.156	0.428	0.479	0.375	0.359	0.367	0.281
2	1.134	1.608	1.062	0.264	0.273	0.188	0.423	0.439	0.375	0.359	0.369	0.281
3	1.136	1.352	1.062	0.310	0.313	0.250	0.425	0.440	0.375	0.357	0.428	0.281
4	1.132	1.574	1.062	0.345	0.361	0.281	0.428	0.478	0.375	0.358	0.363	0.281
5	1.130	1.349	1.062	0.388	0.436	0.344	0.425	0.474	0.375	0.359	0.368	0.281
6	1.129	1.143	1.062	0.430	0.450	0.375	0.426	0.478	0.375	0.358	0.408	0.281
7	1.137	1.979	1.062	0.470	0.501	0.406	0.428	0.454	0.375	0.359	0.413	0.281
8	1.134	1.330	1.062	0.482	0.514	0.438	0.429	0.476	0.375	0.358	0.419	0.281
9	1.131	1.436	1.062	0.596	0.700	0.531	0.427	0.436	0.375	0.358	0.366	0.281
10	1.145	1.255	1.094	0.641	0.766	0.594	0.424	0.447	0.375	0.358	0.365	0.281
11	1.139	1.349	1.062	0.671	0.801	0.594	0.426	1.148	0.375	0.357	0.366	0.281
12	1.139	1.188	1.062	0.737	0.838	0.656	0.426	0.445	0.375	0.358	0.410	0.281
13	1.151	1.188	1.094	0.817	0.899	0.719	0.423	0.439	0.375	0.357	0.893	0.281
14	1.154	1.235	1.094	0.838	0.972	0.781	0.423	0.475	0.375	0.358	0.369	0.281
15	1.145	1.240	1.062	0.849	1.598	0.781	0.427	0.488	0.375	0.359	0.366	0.281
16	1.156	1.450	1.094	0.969	1.043	0.906	0.428	0.446	0.375	0.358	0.367	0.281
17	1.144	1.236	1.062	0.938	1.077	0.875	0.427	0.442	0.375	0.359	0.365	0.281
18	1.176	1.239	1.094	1.012	1.147	0.938	0.425	0.438	0.375	0.360	0.370	0.281
19	1.163	1.712	1.094	1.062	1.978	0.969	0.431	0.440	0.375	0.360	0.386	0.281
20	1.175	1.270	1.125	1.108	1.210	1.031	0.429	0.442	0.375	0.361	0.364	0.281
21	1.188	2.201	1.125	1.176	1.329	1.094	0.426	0.443	0.375	0.359	0.373	0.281
22	1.163	1.370	1.094	1.215	1.314	1.125	0.427	0.478	0.375	0.360	0.413	0.281
23	1.187	1.374	1.125	1.250	1.349	1.156	0.427	0.443	0.375	0.360	0.374	0.281
24	1.172	1.342	1.094	1.317	1.429	1.219	0.429	0.439	0.375	0.360	0.416	0.281
25	1.195	1.318	1.125	1.328	1.460	1.219	0.426	0.528	0.375	0.359	0.369	0.281
26	1.201	1.354	1.125	1.322	1.464	1.250	0.427	0.482	0.375	0.359	0.364	0.281
27	1.197	1.425	1.125	1.418	1.558	1.344	0.427	0.446	0.375	0.360	0.750	0.281
28	1.196	1.454	1.125	1.453	1.591	1.344	0.427	0.437	0.375	0.359	0.917	0.281
29	1.190	1.385	1.125	1.514	1.602	1.469	0.426	0.441	0.375	0.360	0.365	0.281
30	1.243	1.400	1.156	1.518	1.659	1.438	0.428	0.441	0.375	0.355	0.373	0.281
31	1.192	1.345	1.125	1.555	1.705	1.469	0.430	0.440	0.375	0.360	0.370	0.281
32	1.215	1.392	1.125	1.637	1.702	1.500	0.428	0.485	0.375	0.360	0.412	0.281
33	1.229	1.384	1.125	1.674	1.735	1.562	0.427	0.436	0.375	0.358	0.410	0.281
34	1.247	1.397	1.156	1.716	1.826	1.594	0.431	0.440	0.375	0.356	0.388	0.281
35	1.225	2.084	1.156	1.720	1.906	1.625	0.430	0.444	0.375	0.359	0.367	0.281
36	1.232	1.857	1.156	1.786	2.128	1.656	0.426	0.439	0.375	0.358	0.375	0.281
37	1.225	1.407	1.125	1.839	1.905	1.750	0.427	0.488	0.375	0.358	0.366	0.281
38	1.226	1.435	1.156	1.869	2.434	1.750	0.427	0.485	0.375	0.358	0.368	0.281
39	1.223	1.497	1.156	1.849	2.038	1.750	0.428	0.436	0.375	0.359	0.371	0.281
40	1.237	1.357	1.156	1.934	2.104	1.750	0.427	0.477	0.375	0.359	0.368	0.281
41	1.222	1.447	1.156	1.956	2.060	1.875	0.427	0.443	0.375	0.362	0.364	0.281
42	1.254	1.360	1.156	1.988	2.357	1.906	0.428	0.443	0.375	0.359	0.366	0.281
43	1.241	1.391	1.188	2.033	2.155	1.906	0.427	0.488	0.375	0.360	0.367	0.281
44	1.241	1.370	1.188	2.057	2.177	1.969	0.427	1.012	0.375	0.360	0.368	0.281
45	1.257	1.381	1.188	2.100	2.274	1.938	0.427	0.439	0.375	0.362	0.954	0.281
46	1.266	1.350	1.188	2.178	3.041	2.062	0.430	0.440	0.375	0.359	0.368	0.281
47	1.260	1.328	1.188	2.196	2.299	2.062	0.427	0.443	0.375	0.360	0.369	0.281
48	1.285	1.337	1.219	2.203	2.532	2.062	0.428	0.490	0.375	0.361	0.367	0.281
49	1.286	1.682	1.219	2.250	2.605	2.156	0.426	0.435	0.375	0.355	0.370	0.281
50	1.297	1.330	1.219	2.295	2.605	2.156	0.429	0.440	0.375	0.357	0.363	0.281
51	1.303	1.335	1.250	2.343	2.447	2.219	0.430	0.439	0.375	0.360	0.415	0.281
52	1.315	1.640	1.250	2.383	2.871	2.250	0.426	0.480	0.375	0.358	0.368	0.281
53	1.319	1.606	1.250	2.401	2.604	2.281	0.428	0.439	0.375	0.358	0.369	0.281
54	1.342	1.653	1.281	2.438	2.840	2.312	0.430	0.480	0.375	0.358	0.370	0.281
55	1.342	1.387	1.281	2.470	3.336	2.375	0.426	0.441	0.375	0.359	0.414	0.281
56	1.362	1.716	1.281	2.556	2.893	2.438	0.429	0.437	0.375	0.361	0.379	0.281
57	1.364	1.619	1.312	2.573	2.875	2.406	0.428	0.441	0.375	0.362	0.370	0.281
58	1.386	2.069	1.312	2.665	3.150	2.562	0.428	0.436	0.375	0.358	0.365	0.281
59	1.384	1.743	1.312	2.677	2.954	2.531	0.429	0.440	0.375	0.358	0.370	0.281
60	1.411	1.747	1.344	2.911	3.152	2.781	0.428	0.439	0.375	0.358	0.370	0.281
61	1.417	1.761	1.344	2.929	3.240	2.750	0.426	0.483	0.375	0.358	0.368	0.281
62	1.416	2.010	1.344	2.745	3.615	2.656	0.427	0.437	0.375	0.358	0.368	0.281
63	1.453	2.195	1.375	3.046	3.357	2.688	0.427	0.440	0.375	0.359	0.368	0.281
64	1.646	1.654	1.594	3.107	3.208	2.938	0.429	0.443	0.375	0.359	0.407	0.281

Performance test

In performance tests several text files were loaded into memory, then the tested procedure removed spaces 10 time, saving result to a separate memory region.

file	scalar		AVX512VBMI		AVX512VBMI-pext		AVX2
	time [us]	speed-up	time [us]	speed-up	time [us]	speed-up	time [us]	speed-up
tom-sawyer.txt	978		267	3.66	39	25.08	52	18.81
moby-dick.txt	2881		742	3.88	118	24.42	156	18.47
sherlock.txt	1402		376	3.73	55	25.49	72	19.47
census-income.data	123950		46847	2.65	13690	9.05	14574	8.50
weather_sept_85.csv	74037		44637	1.66	9866	7.50	10523	7.04

book	file	file size [B]
The Adventures of Tom Sawyer	`tom-sawyer.txt`	428,104
The Adventures of Sherlock Holmes	`sherlock.txt`	594,933
Moby Dick	`moby-dick.txt`	1,276,201
census-income.data		16,022,599
weather_sept_85.csv		75,137,158

Conclusions

Both AVX2 by Michael and AVX512VBMI by Zach work at constant time.
Although in microbenchmarks the AVX2 variant performs better than the AVX512VBMI code, the real-world cases are handled better by the latter one.
When spaces occupy more than 1/3 of an AVX512 register, the scalar code performs better than the naive vectorized counterpart.

Acknowledgements

As always this work wouldn't be possible without Daniel Lemire, who gave ma access to a Cannon Lake machine.

Source code

Source code is available on github.