Wstęp

Przedstawione niżej metody służą do automatycznego rozmieszczania elementów graficznych reprezentujących węzły w drzewiastych strukturach danych. Dają całkiem przyzwoite wyniki.

Oczywiście istnieją już programy które to robią — jak choćby wyśmienity, darmowy Graphviz — ale też czasem z różnych względów nie zawsze można takowych użyć.

Właściwie w opisanych metodach chodzi wyłącznie o rozmieszczenie węzłów w poziomie. Natomiast odstępy pomiędzy kolejnymi poziomami należy „jakoś” ustalić. W przykładach wziąłem ok. 2-4 wysokości najwyższego węzła; z resztą byłoby dobrze dać końcowemu użytkownikowi jakąś możliwość wpływania na te odstępy.

Założenia wstępne

Węzły są reprezentowane jakąś figurą geometryczną: kołem, prostokątem, prostokątem z zaokrąglonymi rogami, czy czymkolwiek innym — w opisywanych algorytmach nie ma to większego znaczenia, ponieważ brane są tylko skrajne wymiary figur (pudełko otaczające).

Węzły można łatwo dosuwać do innych — każdy ma metodę „ustaw minimalne x na określoną wartość” (setminx).

Z węzła można łatwo sięgnąć do rodzica oraz do pierwszego i ostatniego dziecka, a także do następnego/poprzedniego węzła na tym samym poziomie. Dla osób zaznajomionych z DOM zapewne będą znane takie nazwy własności węzła jak:

• parentNode (rodzic),
• firstChild (pierwsze dziecko „od lewej”),
• lastChild (ostatnie dziecko „najbardziej na prawo”),
• nextSibling (kolejny brat „na prawo”),
• prevSibling (poprzedni brat „na lewo”).

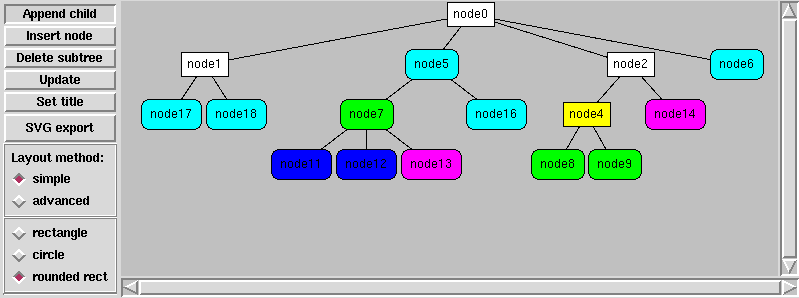
Metoda 1

Zaleta:

1. Do rozmieszczenia węzłów wymaga jednokrotnego przejścia drzewa metodą postorder.

Wady:

1. Przeważnie tworzy szerokie obrazy.
2. Szerokość wszystkich węzłów musi być jednakowa (lub prawie jednakowa) — wydaje mi się, że to akurat nie jest aż tak wielka wada.

Dana jest globalna współrzędna X_C. Wszystkie już rozmieszczone węzły znajdują się po lewej stronie prostej X = X_C, natomiast jeszcze nie przetworzone na pewno zostaną umieszczone na prawo od niej.

Pojedynczy krok algorytmu przedstawia się następująco:

1. Wyznaczanie pozycji węzła.

   • Po przetworzeniu wszystkich potomków środek węzła (na osi X) jest wyznaczany jako średnia arytmetyczna środków pierwszego i ostatniego dziecka.
   • Jeśli natomiast węzeł jest liściem, to zostaje „dosunięty” do X — tzn. minimalna współrzędna pudełka otaczającego jest równa x_min = X_C + s, gdzie s to pewna stała (dająca jakiś odstęp).

2. Następnie uaktualniana jest współrzędna graniczna X_C — nie może być ona mniejsza niż x_max pudełka otaczającego poddrzew danego węzła, ani mniejsza niż x_max pudełka otaczającego samego węzła. W tym celu wystarczy zapamiętać x_max pudełka otaczającego poddrzewa zapisanego w lastChild oraz oczywiście wyznaczyć x_max pudełka otaczającego węzła — i wziąć maksimum obu wartości.

Poniżej funkcja Pythonowa, która realizuje ten algorytm (zadziwiająco krótka, prawda?).

def TreeLayout(node, x, space):
    assert node != None

    if node.childNodes:
        for child in node.childNodes:
            x = TreeLayout(child, x, space)

        node.cx = (node.firstChild.cx + node.lastChild.cx)/2
        return max(x, node.maxx())
    else:
        node.setminx(x + space)
        return node.maxx()

def BinaryTreeLayout(root, space, x=0.0):
    if root is None:
        return x

    root.width = 20

    x = BinaryTreeLayout(root.left,  space, x)
    x = BinaryTreeLayout(root.right, space, x+space)

    if root.left and root.right:
        root.cx = (root.left.cx + root.right.cx)/2
    elif root.left:
        root.cx = roo.left.cx
    elif root.right:
        root.cx = roo.right.cx
    else:
        root.cx    = x
        return root.cx + root.width/2

    return x

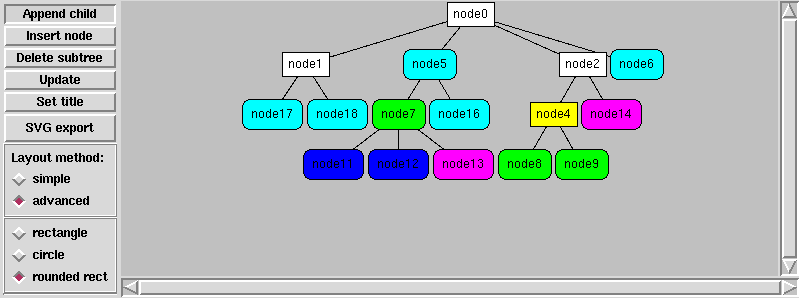
Metoda 2

Przedstawiony niżej algorytm jest nieco bardziej złożony, ale daje lepsze rezultaty.

W pierwszym kroku wszystkie węzły na każdym poziomie są do siebie ściśle dosuwane, tzn. tak że kraniec jednego węzła jest blisko kolejnego (dodawany jest także pewien niewielki odstęp między nimi).

Następnie drzewo jest przeglądane poziomami od dołu — od poziomu przedostatniego aż do korzenia:

• Węzły na każdym poziomie są przeglądane od lewej do prawej; liście są pomijane.

• Jeśli węzeł ma dzieci, to wyznaczany jest jego pożądany środek x_D (wyznaczam średnią środka pierwszego i ostatniego dziecka, można próbować inaczej). Teraz należy rozważyć aktualne położenie środka węzła (x_C) względem obliczonego x_D.

  • Jeśli x_C < x_D (bardziej na lewo) to należy przesunąć w prawo ten węzeł oraz wszystkich jego sąsiadów znajdujących się na prawo — te węzły nie zostały jeszcze przetworzone. Przesunięcie wynosi dx = x_D − x_C.
  • Jeśli x_C > x_D to nie można przesunąć tego węzła w lewo, mogą tam przecież znajdować się inne węzły z tego samego poziomu. Dlatego należy przesunąć w prawo o x_C − x_D jednostek całe poddrzewa tego węzła oraz wszystkich jego sąsiadów z prawej. Dlaczego nie wystarczy tylko tego węzła? Ponieważ na niższych poziomach węzły są już rozmieszczone i trzeba zachować ich wzajemne położenie.

Jak widać sam algorytm nie jest przesadnie skomplikowany. Należy tylko tak zorganizować drzewo, aby można było łatwo odczytać jego poziom oraz wszystkich sąsiadów z prawej. Ja po prostu utworzyłem listy węzłów dla każdego z poziomów, a węzły drzewa zawierają dodatkowe pole informujące o poziomie i położeniu na wspomnianej liście.

def TreeLayout2(node, space):
    if not node:    # empty tree
        return

    class Dummy: pass

    d = Dummy()
    d.levels = []

    def fill_rows(node, level):

        # add node to node's list assigned to certain level
        if len(d.levels) >= level+1:
            d.levels[level].append(node)

        else: # this level is visited first time
            d.levels.append([])
            d.levels[level] = [node]

        # each node has info about it position in d.levels table
        node.index = len(d.levels[level])-1
        node.level = level

        # place new node at end of the row
        if node.index > 0:
            prevnode = d.levels[node.level][node.index-1]
            node.setminx(prevnode.maxx() + space)
        else:
            node.setminx(0) # first node

        # process node's children
        for child in node.childNodes:
            fill_rows(child, level+1)

    def do_layout():

        def translate_child(node, dx):
            for child in node.childNodes:
                translate_tree(child, dx)

        def translate_tree(node, dx):
            node.cx += dx
            for child in node.childNodes:
                translate_tree(child, dx)

        for row in reversed(d.levels[:-1]):
            for parent in row:
                if not parent.hasChildNodes():      # skip leafs
                    continue

                # calucate desired center of node
                cx     = (parent.firstChild.cx + parent.lastChild.cx)/2
                dx     = cx - parent.cx
                if cx > parent.cx:
                    # move dx units right nodes at parent level, starting
                    # from the parent node
                    row1 = d.levels[parent.level]
                    for i in xrange(parent.index, len(row1)):
                        row1[i].cx += dx
                elif cx < parent.cx:
                    # move -dx units right subtrees of parent
                    # and it's neightbours on right
                    row1 = d.levels[parent.level]
                    for i in xrange(parent.index, len(row1)):
                        translate_child(row1[i], -dx)

    fill_rows(node, 0)
    do_layout()

Dodatek

Ponieważ podczas testów powyższych algorytmów nie zawsze odpowiadało mi tworzenie losowych drzew, a jednocześnie opisywanie bezpośrednio w kodzie programu struktury drzewa jest mało przyjemne, dlatego napisałem prosty parser definicji drzew, który akceptuje składnię podobną do tej stosowanej w Graphviz.

# komentarz

# powinien istnieć dokładnie jeden korzeń (nazwę korzenia
# ustala argument funkcji parse_tree_def, domyślnie
# jest to właśnie 'root'

# 1. Tworzenie struktury drzewa:
# węzły A i B są dziećmi korzenia
root -> A
root -> B

# węzeł A ma trzy dzieci
A    -> C
A    -> D
A    -> E

# a węzeł C jedno
C    -> F

# 2. Określanie kształtu węzłów
# tworzenie węzła: nazwa = kształt parametry rozdzielone przecinkami
A    = rectangle "b", 20, 30
B    = rectangle "c", 20, 30
root = circle    "a", 10

# kopiowanie definicje innych węzłów
C    = A
D    = A
E    = C
F    = A

Kolejność tworzenia dowiązań, definiowania kształtu węzłów, ani ich kopiowania nie gra roli.

Procedura zapamiętuje razem z węzłem jaki kształt został mu przypisany (łańcuch classname) i jakie podano parametry (lista parametrów parameters). Aplikacja powinna przetworzyć wynikowe drzewo na swoją własną reprezentację.

Przykładowa funkcja konwertująca:

def convert(node, drawing, level=0):
    """
    Function converts tree returned by parse_tree_def
    into tree used in this demo: it parses parameters
    and creates nodes of given shape and size
    """
    def create(classname, parameters):
        if classname.lower() == "circle":   # "string", r
            return Circle(drawing, float(parameters[1]))
        elif classname.lower() == "rectangle":      # "string", w, h
            return Rectangle(drawing, float(parameters[1]), float(parameters[2]))
        else:
            raise ValueError("Unknown node class '%c'" % classname)

    newnode    = create(node.classname, node.parameters)
    newnode.cy = level*40
    for child in node.childNodes:
        newnode.appendChild( convert(child, drawing, level+1) )

    return newnode

Do pobrania

Demo (Tkinter)

tree_layout-tkdemo.py — program napisany w Tkinterze