Wypełnianie trójkątów i czworokątów wypukłych
| Autor: | Wojciech Muła |
|---|---|
| Dodany: | 5.06.2002 |
| Aktualizacja: | 5.03.2007 |
Contents
Wprowadzenie
Podstawową „jednostką” wypełnienia jest linia pozioma (ang. scanline). Jej granice, tj. początek i koniec wyznaczają jednoznacznie punkty przecięcia poziomej linii (o współrzędnej y) z dwiema krawędziami wielokąta. W przypadku wielokąta niewypukłego tych przecięć mogłoby być więcej — co nie znaczy że nie może być ich dokładnie dwa, ale stwierdzenie tego w ogólnym przypadku jest trudne. (Proponuję zapoznać się również z artykułem o wypełnianiu wielokątów).
Aby wypełnić trójkąt albo wypukły czworokąt należy podzielić figurę na trapezy o podstawach równoległych do osi OX — wypełnianie trapezów/trójkątów spełniających ten warunek jest bardzo proste.
Podział na trapezy wymaga zrzutowania wierzchołków (wzdłuż scanlinów) na naprzeciwległe krawędzie tak jak pokazano to na rysunkach niżej. Ponieważ współrzędna y jest znana, obliczenie współrzędnej x punktu sprowadza się do rozwiązania równania liniowego:
t = (y − y1)/(y2 − y1); x = x1 + t ⋅ (x2 − x1)
Wypełnianie trapezu
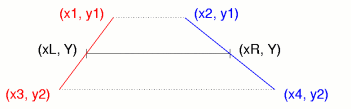
Ponieważ krawędzie trapezu są odcinkami nie ma potrzeby liczyć bezpośrednio przecięcia. Wystarczy obliczyć przyrosty współrzędnej x przy zmianie y o 1.
dxL = (x3 − x1)/dy dxR = (x4 − x2)/dy dy = y2 − y1
a następnie przy każdej zmianie współrzędnej y uaktualniać współrzędne xL i xR zgodnie z zależnościami:
xL = x1 + y ⋅ dxL xR = x2 + y ⋅ dxR y = y1…y2
Dzięki temu wypełnienie trapezu jest bardzo proste, oto przykładowa funkcja:
void fill_segment(int x1, int x2, int x3, int x4, int y1, int y2) {
float dy = y2-y1;
float dxl = float(x3-x1)/dy;
float dxl = float(x4-x2)/dy;
float xl = x1;
float xr = x2;
for (int y=y1; y<y2; y++) {
line_h(xl, xr, y);
xl += dxl;
yl += dxr;
}
}
Ponieważ może zdarzyć się tak, że xl > xr więc funkcja line_h musiałaby uwzględniać i takie przypadki: w najlepszym razie poprzez zamianę kolejność x-ów, w najgorszym stawiać piksele z lewej do prawej, bądź z prawej do lewej. Można tego uniknąć i już na wstępie określić która ze współrzędnych jest „bardziej na lewo”:
- x1 != x2 — w tym przypadku decyduje oczywiście zależność x1 > x2,
- x1 == x2 — natomiast w tym zależność dxl > dxr.
if (((x1 != x2) && (x1 > x2)) || (x1 == x2) && (dxl > dxr)) {
swap(dxl, dxr);
swap( xl, xr);
}
Wypełnianie trójkątów
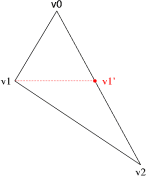
Najpierw należy posortować wierzchołki wg rosnącego y; sortowanie najlepiej przeprowadzić metodą bąbelkową, trzeba ledwie trzech porównań:
if (P0.y < P1.y) swap(P0, P1); if (P0.y < P2.y) swap(P0, P2); if (P1.y < P2.y) swap(P1, P2);
W efekcie otrzymujemy posortowane wierzchołki w kolejności P0, P1, P3, gdzie P0.y = min. Następnie wierzchołek 1 rzutowany jest na krawędź 0-2, otrzymujemy nowy punkt P11.
Ostatnim etapem jest wypełnienie dwóch obszarów (rosnący y):
- trójkąta P0 − P1 − P11
- trójkąta P1 − P11 − P2
Wypełnianie czworokątów
Tutaj nie można już wprost posortować wierzchołków względem współrzędnej y, ale należy znaleźć dwa skrajne wierzchołki: o minimalnej i maksymalnej współrzędnej y.
Jeśli wierzchołki dane są jako lista P0, P1, P2, P3, wskazać dwa indeksy (zakres 0-3) A — najmniejsza wartość y oraz D — największa. Zostają dwa wierzchołki — ich indeksy niech będą B oraz C.
Do rozpatrzenia są dwa przypadki, gdy skrajne wierzchołki PA i PD należą do jednej krawędzi (1), czy też nie (2).
Przypadek 1.
Tak jest wtedy, gdy |A − D| = 0 lub |A − D| = 3. Należy znaleźć wierzchołek, który jest połączony z dolnym punktem PA — oznaczmy go PB (PC jest połączony krawędzią z PD, górnym punktem). Ponieważ liczba kombinacji wartości A i D wynosi w tym przypadku 8, można bez problemu stablicować wybór B i C.
Następnie wyznaczane są rzuty PB i PC na krawędź PAPD: wynikiem są dwa punkty PB1 i PC1.
Ostatnim etapem jest wypełnienie trzech obszarów (rosnący y):
- trójkąt PA − PB − PB1
- trapez PB − PB1 − PC − PC1
- trójkąt PC − PC1 − PD
Przypadek 2.
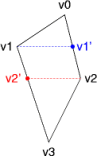
Tutaj w prostszy sposób określane są indeksy B i C. Punkt PB, to ten który ma mniejszą współrzędną y, a indeksy B i C określa zależność (A ± 1) mod 4.
Teraz wyznaczane są rzuty:
- punktu PB na krawędź PAPC (PB1)
- punktu PC na krawędź PBPD (PC1)
Ostatnim etapem jest wypełnienie trzech obszarów (rosnący y):
- trójkąt PA − PB − PB1
- trapez PB − PB1 − PC − PC1
- trójkąt PC − PC1 − PD